cách xác định hàm số đồng biến nghịch biến

Trong toán học tập, tất cả chúng ta cần được biết phương pháp phân biệt hàm số đồng trở thành và nghịch tặc trở thành. Vậy hàm số đồng trở thành Lúc nào? Làm thế nào là nhằm xét tính đồng trở thành hoặc nghịch tặc trở thành bên trên một hàm số cụ thể? Bài ghi chép tại đây tiếp tục khiến cho bạn hiểu rõ hàm số đồng trở thành lúc nào, giống như thích nghi với một trong những dạng bài xích luyện về đồng trở thành, nghịch tặc trở thành. Hãy nằm trong bọn chúng bản thân dò la hiểu những kỹ năng cơ phiên bản của công tác học tập Trung học tập Phổ thông tức thì nhé

Định nghĩa hàm số đồng trở thành và nghịch tặc biến

Cách khái niệm hàm số đồng trở thành và nghịch tặc trở thành được tiến hành như sau:

Bạn đang xem: cách xác định hàm số đồng biến nghịch biến

Hàm số đồng trở thành là gì?

Cho K là ký hiệu của một khoảng tầm, một quãng hoặc nửa khoảng tầm ngẫu nhiên. Giả sử: Hàm số hắn = f(x) được xác lập bên trên K.

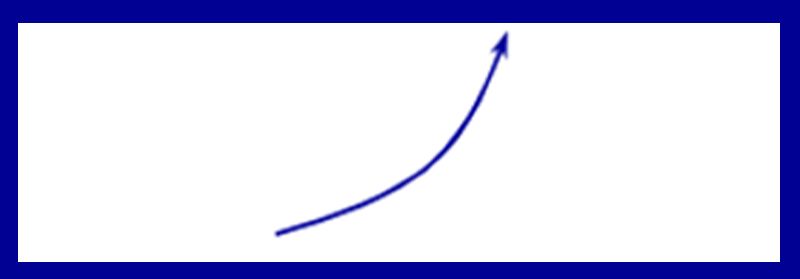
Lúc này, tớ nói: Hàm số hắn = f(x) được gọi là đồng biến (tăng) trên K nếu:

$\forall x_1,x_2\in K,x_1<x_2\Rightarrow f\left(x_1\right)<f\left(x_2\right)$

Ký hiệu cho tới hàm số đồng trở thành là vệt mũi thương hiệu phía lên bên trên.

Hàm số nghịch tặc trở thành là gì?

Tương tự động với hàm số đồng trở thành, Lúc xét hàm số nghịch tặc trở thành, tớ gọi K là ký hiệu của một khoảng tầm, một quãng hoặc nửa khoảng tầm. Hàm số hắn = f(x) được xác lập bên trên K.

Lúc này, hàm số hắn = f(x) được gọi là nghịch tặc trở thành (giảm) bên trên K nếu:

 $\forall x_1,x_2\in K,x_1<x_2\Rightarrow f\left(x_1\right)>f\left(x_2\right)$

Ký hiệu cho tới hàm số nghịch tặc trở thành là vệt mũi thương hiệu phía xuống bên dưới.

Khi nào là hàm số đồng trở thành, nghịch tặc biến

Khi xét tính đồng trở thành và nghịch tặc trở thành của một hàm số chắc chắn, tớ cần thiết Note những ĐK bên dưới đây:

• Hàm số hắn = f(x) đồng trở thành bên trên K Lúc và chỉ khi: 

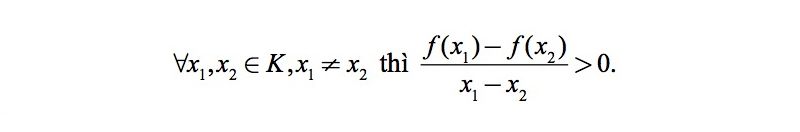
• Hàm số hắn = f(x) nghịch tặc trở thành bên trên K Lúc và chỉ khi: 

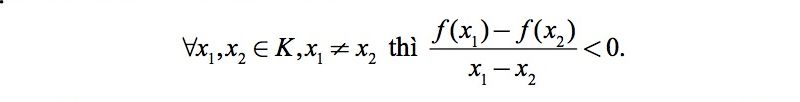
Công thức xét tính đồng trở thành, nghịch tặc biến

Công thức xét tính đồng trở thành, nghịch tặc trở thành được tiến hành theo đòi công việc như sau:

• Bước 1: Tìm luyện xác lập D của hàm số
• Bước 2: Tính đạo hàm của hàm số vẫn cho tới f'(x)
• Bước 3: Tìm những điểm tuy nhiên bên trên cơ f′(x) = 0 hoặc f′(x) ko xác định
• Bước 4: Sắp xếp những điểm theo đòi trật tự tăng dần
• Bước 5: Lập bảng trở thành thiên 
• Bước 6: Căn cứ nhập bảng trở thành thiên, tiếp sau đó tớ rút rời khỏi tóm lại về khoảng tầm đồng trở thành, nghịch tặc trở thành của hàm số đã và đang được nêu nhập đề bài

Bài luyện hàm số đồng trở thành nghịch tặc biến

Sau đấy là một trong những dạng bài xích luyện về hàm số đồng trở thành, nghịch tặc trở thành bên trên một khoảng tầm (đoạn hoặc nửa khoảng tầm nhất định). Các chúng ta cũng có thể xem thêm nhằm dò la nắm rõ rộng lớn về dạng toán này.

• Bài luyện 1: Cho hàm số hắn = x⁴ – 2x² + 3 . Kết luận nào là sau đấy là đúng?

A. Hàm số nghịch tặc trở thành bên trên khoảng tầm (-∞; -1) ∩ (0; 1)

B. Hàm số đồng trở thành bên trên khoảng tầm (-1; 0) ∪ (1; +∞)

C. Hàm số nghịch tặc trở thành bên trên khoảng tầm (-∞; -1) ∪ (0; 1)

D. Hàm số đồng trở thành bên trên những khoảng tầm (-1; 0) và (1; +∞)

Đáp án: D

• Bài luyện 2: Chọn đáp án đúng: Khoảng nghịch tặc trở thành của hàm số hắn = x³/3 – 2x² + 3x + 5 là?

A. (1; 3)     B. (-∞; 1) ∪ (3; +∞)    C. (-∞; 1) và (3; +∞)     D. (1; +∞)

Đáp án: A

Xem thêm: sau khi xuyên thư ta bị nữ chủ đánh dấu

• Bài luyện 3: Cho hàm số hắn = x³ – (m + 1)x² – (m² – 2m)x + 2020. Tìm m nhằm hàm số vẫn cho tới nghịch tặc trở thành bên trên khoảng tầm (0; 1).

Đáp án: Ta có:

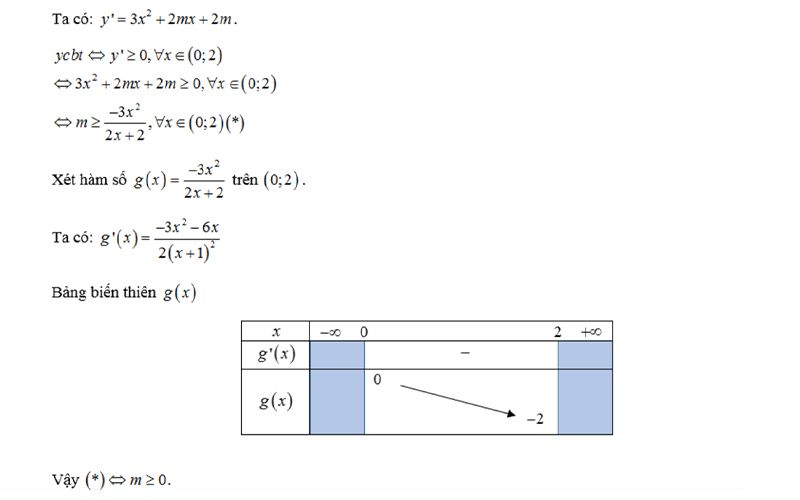
• Bài luyện 4: Cho hàm số hắn = x³ + mx² + 2mx + 3. Tìm ĐK của m nhằm hàm số đồng trở thành bên trên khoảng tầm (0; 2).

Đáp án:

• Bài luyện 5: Hàm số nào là tại đây đồng trở thành bên trên R?

A. y = x³ – 2x – 2.

B. y = x²⁰¹⁹ + x²⁰²¹ – 2.

C. y = -x³ + x + 3.

D. y = x²⁰¹⁸ + x²⁰²⁰ – 2.

Đáp án: B

• Bài luyện 6: Tìm toàn bộ những độ quý hiếm thực của thông số m sao cho tới hàm số $y=f\left(x\right)=x+m\cos \mathrm{x\; luôn}$ đồng trở thành bên trên $R$?

A. $\left|m\right|\le 1$

B. $m>\; (\frac{\sqrt{\mathrm{3)/}}}{2}$

C. $\left|m\right|\ge 1$

D. $m<\frac{\mathrm{1/}}{2}$

Đáp án: A

• Bài luyện 7: Tìm những khoảng tầm đồng trở thành và nghịch tặc trở thành của những hàm số bên dưới đây:

a) hắn = x³ − 3x² + 2

b) hắn = x⁴ − 2x²

Đáp án:

a) Tập xác lập của hàm số hắn = x³ − 3x² + 2 là: D = R

Ta có:

b) Tập xác lập của hàm số hắn = x⁴ − 2x² là: D = R

Xem thêm: nhân ngư rơi xuống tiểu thuyết

Ta có:

Xem thêm:

• Hỗn số là gì? Khái niệm, phương pháp tính lếu số và bài xích luyện ví dụ minh họa
• Công thức tính diện tích S tam giác, hình thoi, hình vuông vắn, hình chữ nhật, hình tròn
• Các cơ hội học tập xuất sắc hóa hiệu suất cao, sớm nhất cho tất cả những người tổn thất gốc

Thông qua loa nội dung bài viết bên trên, kỳ vọng chúng ta vẫn hiểu rõ hàm số đồng trở thành lúc nào, giống như thích nghi và xem thêm được một trong những dạng bài xích luyện tương quan cho tới dạng toán đồng trở thành, nghịch tặc trở thành. Chúc các bạn lượm lặt được thành quả cao nhập toàn bộ những môn học tập. Và hãy nhớ là đón gọi nhiều nội dung bài viết hữu ích không giống bên trên Bamboo School chúng ta nhé!